SERE Style

Up until now, we have seen PSL properties that are built of Boolean expres- sions and temporal operators in LTL style. Another way to build properties is to use SEREs – Sequential Extended Regular Expressions. SEREs are similar in spirit to standard regular expressions, like those used for pattern matching in many applications. One difference is that the atoms of a SERE are Boolean expressions, whereas the atoms of a standard regular expression are single characters.

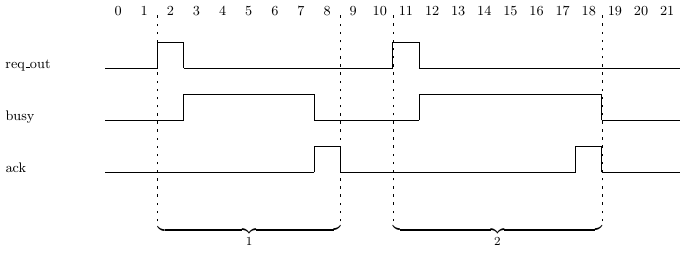
A SERE is typically enclosed in curly braces, and the atoms of the SERE are typically separated by semi-colons. For instance, {a;b;c} is a SERE, and SERE 5.1a is a more complicated SERE. SERE 5.1a describes a sequence of cycles in which (req_out && !ack) is asserted on the first cycle, then (busy && !ack) is asserted for zero or more cycles, indicated by the consecutive repetition operator [*], and finally ack is asserted. Thus, SERE 5.1a matches the sequence of cycles labeled as “1” in Trace 5.1(i).

Don’t be tempted into reading more into a SERE than is actually there: SERE 5.1a matches the sequence of cycles labeled as “2” in Trace 5.1(i) as well. SERE 5.1a does not prohibit the assertion of busy during the last cycle of the SERE. If it is important to exclude such behavior, busy must be mentioned explicitly, as shown in SERE 5.1b. SERE 5.1b matches the sequence of cycles labeled as “1” shown in Trace 5.1(i), but does not match the sequence of cycles labeled as “2” in that trace.

How is a SERE used? First, since a SERE is a property, it can be used as a sub-property. For example, Property 5.2a holds if whenever there is an assertion of req_in && gnt then starting on the next cycle we see a sequence of cycles matching SERE 5.1a. Property 5.2a holds on Trace 5.2(i).

NOTE: A SERE is a property, but a property is not a SERE. Thus, while you can use a SERE as an operand of a temporal operator, you cannot embed a temporal operator such as always or next inside of a SERE.

Suppose now that we have a situation similar to that of Property 5.2a, but in which a grant (assertion of signal gnt) is given the cycle after the assertion of req_in. We could try to replace the Boolean expression req_in && gnt with the temporal expression req_in && next gnt, as in Property 5.3a. However, remember the lesson of Section 3.4: in Property 5.3a the current cycle of the left-hand side (req_in && next gnt) is the same as the current cycle of the right-hand side (because they are connected by the Boolean operator ->). Thus, the current cycle of gnt (which is the operand of a next operator) is the same as the current cycle of the SERE (which is also the operand of next operator). This is slightly confusing, and indeed Property 5.3a is not in the simple subset of PSL discussed in Chapter 9.

Let’s modify Property 5.3a as shown in Property 5.3b. Now a single next operator is applied to both gnt and the SERE, which are both operands of the -> operator. Property 5.3b is equivalent to Property 5.3a, but is in the simple subset, making the timing between gnt and the SERE easier to see. If we mean that the current cycle of the SERE should be the cycle after that of gnt, we can manipulate Property 5.3b by adding a next as in Property 5.3c. However, the suffix implication operators provide a much easier way.

(i) SERE 5.1a matches both 1 and 2. SERE 5.1b matches 1, but not 2.
{(req_out && !ack) ; (busy && !ack)[*] ; ack} (5.1a) {(req_out && !ack) ; (busy && !ack)[*] ; ack && !busy} (5.1b)
Fig. 5.1: Two simple SEREs

(i) Property 5.2a holds
always ((req_in && gnt) -> (5.2a) next {(req_out && !ack) ; (busy && !ack)[*] ; ack})
Fig. 5.2: A SERE is a property

always ((req_in && next gnt) ->                            (5.3a)
   next {(req_out && !ack) ; (busy && !ack)[*] ; ack})
always (req_in -> next (gnt ->                             (5.3b)
   {(req_out && !ack) ; (busy && !ack)[*] ; ack}))
always (req_in -> next (gnt ->                             (5.3c)
   next {(req_out && !ack) ; (busy && !ack)[*] ; ack}))

5.1 Suffix implication (|-> and |=>)

The suffix implication operators (|-> and |=>) provide a way to link two SEREs in such a way that the right-hand side starts when the left-hand side finishes. The overlapping suffix implication operator (|->) interprets “when the left-hand side finishes” as “at the same cycle as the cycle in which the left-hand side finishes”, while the non-overlapping suffix implication operator (|=>) interprets it as “the cycle after the cycle in which the left-hand side fin- ishes”. Thus, Property 5.4a is equivalent to Property 5.3b, and Property 5.4b is equivalent to Property 5.3c. Both Property 5.4a and Property 5.4b are eas- ier to grasp than the equivalent property without suffix implication, and both belong to the simple subset, discussed in Chapter 9.

always {req_in;gnt} |-> (5.4a) {(req_out && !ack) ; (busy && !ack)[*] ; ack} always {req_in;gnt} |=> (5.4b) {(req_out && !ack) ; (busy && !ack)[*] ; ack}
Fig. 5.4: Suffix implication

Recall that the logical implication operator (->) can be understood as an if-then expression, with the else-part being implicitly true. The suffix implica- tion operators (|-> and |=>) can be understood the same way. The difference between the logical implication operator (->) and the suffix implication op- erators (|-> and |=>) is in the timing relationship between the if- and the then-parts. While the current cycle of the then-part of a logical implication operator (->) is the same as the current cycle of its if-part, the current cycle of the then-part of a suffix implication operator (|-> or |=>) is the first cycle of the suffix of the trace that remains once the if-part has been seen. 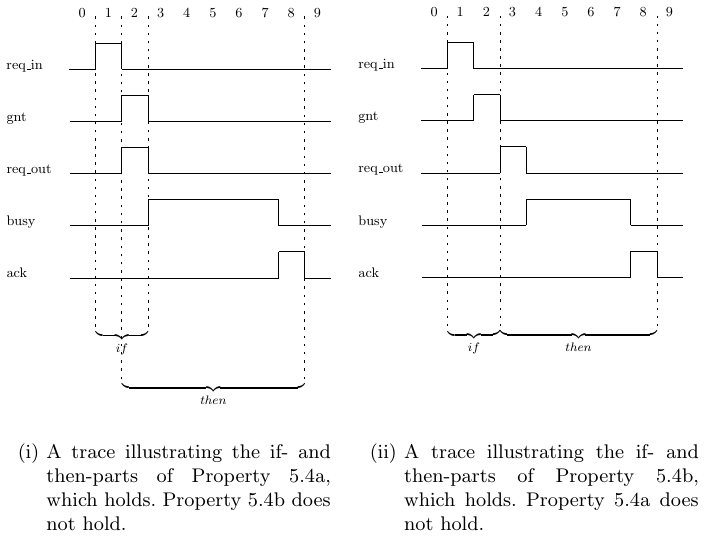This is illustrated for Properties 5.4a and 5.4b in Traces 5.4(i) and 5.4(ii).

(i) A trace having multiple if-then pairs. Property 5.5a holds.
always {req_in;gnt} |=> (5.5a) {(req_out && !ack) ; (busy && !ack)[*] ; ack}
Fig. 5.5: The if-part of another if-then pair may begin before the if-part or the then-part of a previous if-then pair has completed

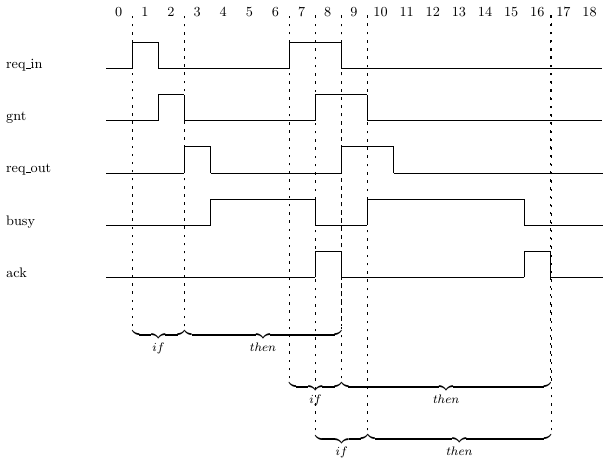
In Traces 5.4(i) and 5.4(ii) there is a single assertion of signal req_in. If there are multiple assertions of req_in, then of course we will be able to identify multiple if-then pairs, as shown in Trace 5.5(i). Note that the if-part of another if-then pair may begin before the if-part or the then-part of a previous if-then pair has completed. For instance, the second if-then pair starts at cycle 7, before the then-part of the first if-then pair has completed. The third if- then pair starts at cycle 8, before the then-part of the first if-then pair has completed, and before the if-part of the second if-then pair has completed. We have seen this kind of overlapping previously, in Traces 2.2(ii) and 2.3(iii). Note that in Trace 5.5(i), the assertion of ack at cycle 16 completes the then- part of the second and of the third if-then pair. For a deeper discussion of this phenomenon, see Section 13.4.2.

Properties 5.6a and 5.6b hold on Trace 5.6(i) because there is no sequence of cycles matching the left-hand side, thus the else-parts default to true at every cycle.

(i) Properties 5.6a and 5.6b both hold
always {req_in;gnt} |-> (5.6a) {(req_out && !ack) ; (busy && !ack)[*] ; ack} always {req_in;gnt} |=> (5.6b) {(req_out && !ack) ; (busy && !ack)[*] ; ack}
Fig. 5.6: The else-part of a suffix implication defaults to true

5.2 Weak and strong SEREs