PSL/A Practical Introduction to PSL/Basic Temporal Properties
- 1. Introduction (en)
- 2. Basic Temporal Properties (en)
- 3. Some Philosophy (en)
- 4. Weak vs. Strong Temporal Operators (en)
- 5. SERE Style (en)
Содержание |
Basic Temporal Properties
While the Boolean layer consists of Boolean expressions that hold or do not
hold at a given cycle, the temporal layer provides a way to describe relationships
between Boolean expressions over time. A PSL assertion typically looks
in only one direction – forwards from the first cycle (although it is possible
to look backwards using built-in functions such as prev(), rose() and
fell()). Thus, the simple PSL assertion assert a; states that a should hold
at the very first cycle, while the PSL assertion assert always a; states that
a should hold at the first cycle and at every cycle following the first cycle –
that is, at every cycle.
By combining the temporal operators in various ways we can state properties
such as “every request receives an acknowledge”, “every acknowledged
request receives a grant within four to seven cycles unless the request is canceled
first”, “two consecutive writes should not be to the same address”, and
“when we see a read request with tag equal to i, then on the next four data
transfers we expect to see a tag of i”.
The temporal layer is composed of the Foundation Language (FL) and the Optional Branching Extension (OBE). The FL is used to express properties of single traces, and can be used in either simulation or formal verification. The OBE is used to express properties referring to sets of traces, for example “there exists a trace such that ...”, and is used in formal verification. In this book we concentrate on the Foundation Language.
The Foundation Language itself is composed of two complementary styles – LTL style, named after the temporal logic LTL on which PSL is based, and SERE style, named after PSL’s Sequential Extended Regular Expressions, or SEREs. In this chapter we present the basic temporal operators of LTL style. We provide only a taste – enough to get the basic idea and to give some context to the philosophical issues that we discuss next.
Throughout this book, we make extensive use of examples. Each example property or assertion and its associated timing diagram (which we term a trace) are grouped together in a figure. Such a figure will contain one or more traces numbered with a parenthesized lower case Roman numeral, and one or more properties numbered by appending a lower case letter to the figure number. For instance, Figure 2.1 contains Trace 2.1(i) and Assertions 2.1a, 2.1b, and 2.1c.
2.1 The always and never operators
We have already seen the basic temporal operators always and never. Most
PSL properties will start with one or the other. This is because a “bare”
(Boolean) PSL property refers only to the first cycle of a trace. For example,
Assertion 2.1a requires only that the Boolean expression !(a && b) hold at
the first cycle. Thus, Assertion 2.1a holds on Trace 2.1(i) because the Boolean
expression !(a && b) holds at cycle 0. In order to state that we want it to
hold at every cycle of the design, we must add the temporal operator always
to get Assertion 2.1b. Assertion 2.1b does not hold on Trace 2.1(i) because
the Boolean expression !(a && b) does not hold at cycle 5. Equivalently, we
could have swapped the always operator and the Boolean negation ! with
never, to get Assertion 2.1c.
|
|---|
| (i) Assertion 2.1a holds, but 2.1b and 2.1c do not |
assert !(a && b); (2.1a) assert always !(a && b); (2.1b) assert never (a && b); (2.1c) |
| Fig. 2.1: The always and never operators |
Both Assertion 2.1b and Assertion 2.1c state that signals a and b are
mutually exclusive. Obviously, anything that can be stated with the always
operator can be stated with the never operator and vice versa, simply by
negating the operand when switching between always and never. PSL provides
both operators for convenience, as sometimes it is more natural to state
the property in the positive (that is, stating what must hold at all cycles)
and sometimes in the negative (that is, what must not hold for any cycle). In
general, there are many ways to state any property in PSL. We will see other
examples throughout the rest of this book.
2.2 The next operator
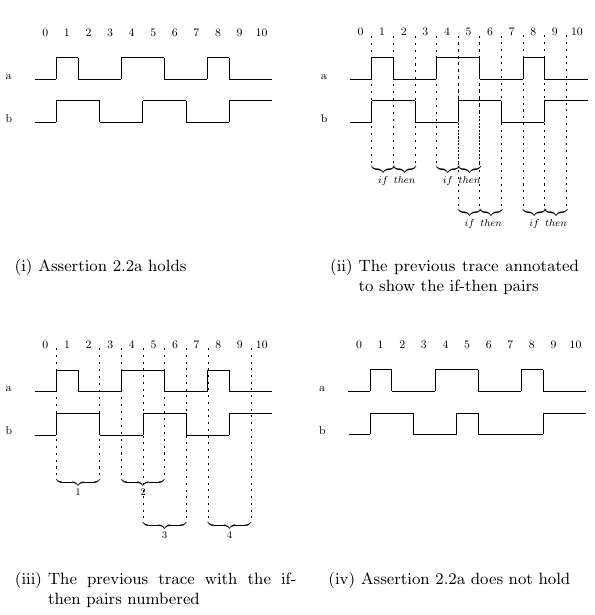
Another temporal operator is the next operator. It indicates that the property
will hold if its operand holds at the next cycle. For instance, Assertion 2.2a
states that whenever a holds, then b should hold in the next cycle. Assertion
2.2a uses another important operator, the logical implication operator
(->). While the logical implication operator is a Boolean and not a temporal
operator (it does not link two sub-properties over time), it plays a very important
role in many temporal properties. A logical implication prop1 -> prop2
holds if either prop1 does not hold or prop2 holds. A good way to think of it
is like an if-then expression, with the else-part being implicitly true. That is,
prop1 -> prop2 can be understood as “if prop1 then prop2 else true”. Thus,
the sub-property a -> next b in our example holds if either a does not hold
(because then the property defaults to true) or if a holds and also next b
holds. By adding an always operator, we get a property that holds if the
sub-property a -> next b holds at every cycle. Thus, Assertion 2.2a states
that whenever a holds, b must hold at the next cycle. Assertion 2.2a holds on
Trace 2.2(i) because every assertion of signal a is followed by an assertion of
signal b. This is shown in the “if” and “then” annotations on Trace 2.2(ii).
The “additional” assertions of signal b at cycles 1 and 10 are allowed by Assertion
2.2a, because it says nothing about the value of b in cycles other than
those following an assertion of a.
Note that the cycles involved in satisfying one assertion of signal a may
overlap with those involved in satisfying another assertion. For example, consider
Trace 2.2(iii), which is simply Trace 2.2(ii) with the if-then pairs numbered.
There are four assertions of signal a on Trace 2.2(iii), and thus four
associated cycles in which b must be asserted. Each pair of cycles (an assertion
of a followed by an assertion of b) is numbered in Trace 2.2(iii). Consider
pairs 2 and 3. Signal a is asserted at cycle 4 in pair 2, thus signal b needs to
be asserted at cycle 5 in order for Assertion 2.2a to hold. Signal a is asserted
at cycle 5 in pair 3, thus requiring that signal b be asserted at cycle 6. Pairs
2 and 3 overlap, because while we are looking for an assertion of signal b at
cycle 5 in order to satisfy the assertion of a at cycle 4, we see an additional
assertion of signal a that must be considered.
Assertion 2.2a does not hold on Trace 2.2(iv) because the third assertion
of signal a, at cycle 5, is missing an assertion of signal b at the following cycle.
|
|---|
assert always (a -> next b); (2.2a) |
| Fig. 2.2: The next and logical implication operators |
2.3 Variations on next including next_event
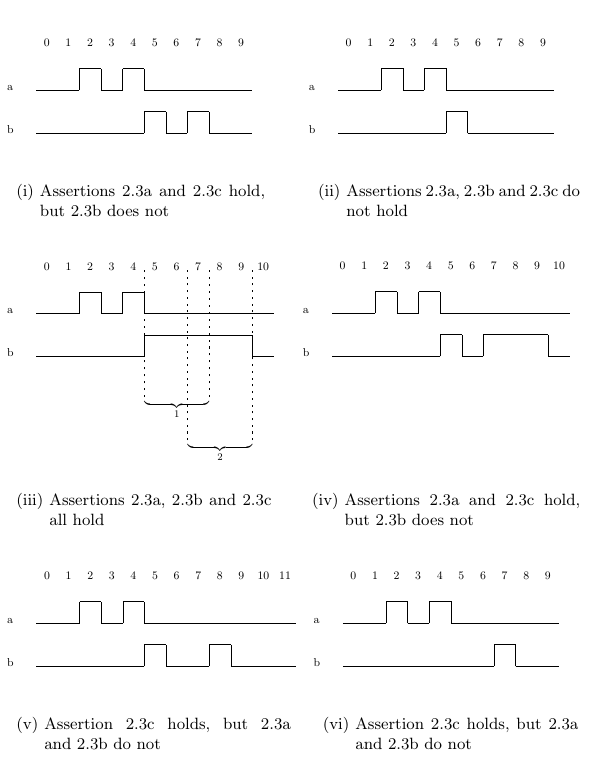
A next property holds if its operand holds in the next cycle. Variations on the
next operator allow you to specify the nth next cycle, and ranges of future
cycles. A next[n] property holds if its operand holds in the nth next cycle.
For example, Assertion 2.3a states that whenever signal a holds, signal b holds
three cycles later. Assertion 2.3a holds on Traces 2.3(i), 2.3(iii), and 2.3(iv),
while it does not hold on Traces 2.3(ii) or 2.3(v) because of a missing assertion
of signal b at cycle 7, and does not hold on Trace 2.3(vi) because of a missing
assertion of signal b at cycle 5.
|
|---|
assert always (a -> next[3] (b)); (2.3a) assert always (a -> next_a[3:5] (b)); (2.3b) assert always (a -> next_e[3:5] (b)); (2.3c) |
Fig. 2.3: Операторы next[n], next_a[i:j] и next_e[i:j]
|
A next_a[i:j] property holds if its operand holds in all of the cycles from
the ith next cycle through the jth next cycle, inclusive. For example, Assertion
2.3b states that whenever signal a holds, signal b holds three, four and
five cycles later. It holds on Trace 2.3(iii) and does not hold on Traces 2.3(i),
2.3(ii), 2.3(iv), 2.3(v), or 2.3(vi).
Previously we discussed the fact that the cycles involved in satisfying one
assertion of signal a may overlap those involved in satisfying another assertion
of a. Trace 2.3(iii) has been annotated to emphasize this point for Assertion
2.3b. Signal b must be asserted in cycles 5 through 7 (marked as “1”)
because of the assertion of a at cycle 2, and must be asserted in cycles 7
through 9 (marked as “2”) because of the assertion of a at cycle 4.
A next_e[i:j] property holds if there exists a cycle from the next i
through the next j cycles in which its operand holds. For example, Assertion
2.3c states that whenever signal a holds, signal b holds either three, four,
or five cycles later. There is nothing in Assertion 2.3c that prevents a single
assertion of signal b from satisfying multiple assertions of signal a, thus it
holds on Trace 2.3(vi) because the assertion of b at cycle 7 comes five cycles
after the assertion of signal a at cycle 2, and three cycles after the assertion
of signal a at cycle 4. We examine the issue of specifying a one-to-one
correspondence between signals in Section 13.4.2.
Assertion 2.3c also holds on Traces 2.3(i), 2.3(iii), 2.3(iv), and 2.3(v),
since there are enough assertions of signal b at the appropriate times. In
Traces 2.3(i), 2.3(iii), and 2.3(iv) there are more than enough assertions of b
to satisfy the property being asserted (in Trace 2.3(i), the assertion of b at
cycle 7 is enough, because it comes five cycles after the assertion of a at cycle
2, and three cycles after the assertion of a at cycle 4). In Trace 2.3(v) there
are just enough assertions of b to satisfy the requirements of Assertion 2.3c.
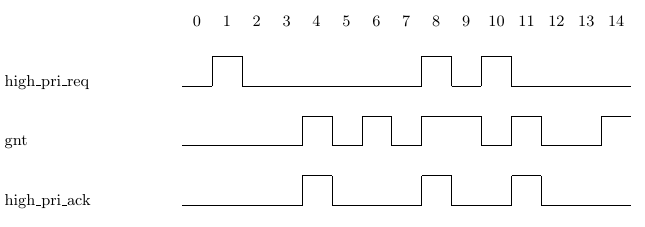
The next_event operator is a conceptual extension of the next operator.
While next refers to the next cycle, next_event refers to the next
cycle in which some Boolean condition holds. For example, Assertion 2.4a
expresses the requirement that whenever a high priority request is received
(signal high_pri_req is asserted), then the next grant (assertion of signal
gnt) must be to a high priority requester (signal high_pri_ack is asserted).
Assertion 2.4a holds on Trace 2.4(i). There are two assertions of signal
high_pri_req, the first at cycle 1 and the second at cycle 10. The associated
assertions of gnt occur at cycles 4 and 11, respectively, and high_pri_ack
holds in these cycles.
The next_event operator includes the current cycle. That is, an assertion
of b in the current cycle will be considered the next assertion of b in the
property next_event(b)(p). For instance, consider Trace 2.4(ii). Trace 2.4(ii)
is similar to Trace 2.4(i) except that there is an additional assertion of
high_pri_req at cycle 8 and two additional assertions of gnt at cycles 8
and 9, one of which has an associated high_pri_ack. Assertion 2.4a holds on
Trace 2.4(ii) because the assertion of gnt at cycle 8 is considered the next
assertion of gnt for the assertion of high_pri_req at cycle 8. If you want to
exclude the current cycle, simply insert a next operator in order to move the
current cycle of the next_event operator over by one, as in Assertion 2.4b.
Assertion 2.4b does not hold on Trace 2.4(ii). Because of the insertion of the
next operator, the relevant assertions of gnt have changed from cycles 4, 8
and 11 for Assertion 2.4a to cycles 4, 9 and 11 for Assertion 2.4b, and at cycle
9 there is no assertion of high_pri_ack in Trace 2.4(ii).
|
|---|
| (i) Assertions 2.4a and 2.4b hold |
|
| (ii) Assertion 2.4a holds, but 2.4b does not |
assert always (high_pri_req -> (2.4a) next_event(gnt)(high_pri_ack)); assert always (high_pri_req -> (2.4b) next next_event(gnt)(high_pri_ack)); |
Fig. 2.4: next_event
|
Just as we can use next[i] to indicate the ith next cycle, we can use
next_event(b)[i] to indicate the ith occurrence of b. For example, in order
to express the requirement that every time a request is issued (signal req is
asserted), signal_last ready must be asserted on the fourth assertion of signal
ready, we can code Assertion 2.5a. Assertion 2.5a holds on Trace 2.5(i). For
the first assertion of req, at cycle 1, the four assertions of ready happen
to come immediately and in consecutive cycles. For the second assertion of
req, at cycle 7, the four assertions of ready do not happen immediately and
do not happen consecutively either – they are spread out over seven cycles,
interspersed with cycles in which ready is deasserted. However, the point is
that in both cases, signal last_ready is asserted on the fourth assertion of
ready, thus Assertion 2.5a holds on Trace 2.5(i).
|
|---|
| (i) Assertion 2.5a holds |
assert always (req -> (2.5a) next event(ready)[4](last ready)); |
| Fig. 2.5: next event[n] |
As with next_a[i:j] and next_e[i:j], the next_event operator also
comes in forms that allow it to indicate all of a range of future cycles, or the existence
of a future cycle in such a range. The form next_event_a(b)[i:j](f)
indicates that we expect f to hold on all of the ith through jth occurrences
of b. For example, Assertion 2.6a indicates that when we see a read request
(assertion of signal read_request) with tag equal to i, then on the next four
data transfers (assertion of signal data), we expect to see tag i. Assertion 2.6a
uses the forall construct, which we will examine in detail later. For now, suffice
it to say that Assertion 2.6a states a requirement that must hold for all
possible values of the signal tag[2:0]. Assertion 2.6a holds on Trace 2.6(i)
because after the first assertion of signal read_request, where tag[2:0] has
the value 4, the value of tag[2:0] is also 4 on the next four assertions of
signal data (at cycles 5, 9, 10 and 11). Likewise, on the second assertion of
signal read_request, where tag[2:0] has the value 5, the value of tag[2:0]
is also 5 on the next four assertions of signal data (at cycles 17 through 20).
In order to indicate that we expect something to happen on one of the next
ith to jth cycles, we can use the next_event_e(b)[i:j](f) operator, which
indicates that we expect f to hold on one of the ith through jth occurrences of
b. For example, consider again Assertion 2.4a. It requires that whenever a high
priority request is received, the next grant must be to a high priority requester.
Suppose instead that we require that one of the next two grants be to a high
priority requester. We can express this using Assertion 2.7a. Assertion 2.7a
holds on Trace 2.7(i) because every time that signal high_pri_req is asserted,
signal high_pri_ack is asserted on one of the next two assertions of gnt.
The syntax of the range specification for all operators – including those
we have not yet seen – is flavor dependent. In the Verilog, SystemVerilog and
SystemC flavors, it is [i:j]. In the VHDL flavor it is [i to j]. In the GDL
flavor it is [i..j].
|
|---|
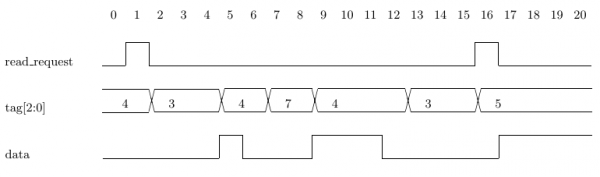
| (i) Assertion 2.6a holds |
assert forall i in {0:7}: (2.6a)
always ((read_request && tag[2:0]==i) ->
next_event_a(data)[1:4](tag[2:0]==i));
|
Fig. 2.6 next_event a[i:j]
|
2.4 The until and before operators
|
|---|
| (i) Assertion 2.7a holds |
assert always (high_pri_req -> (2.7a) next_event_e(gnt)[1:2](high_pri_ack)); |
Fig. 2.7: next_event e[i:j]
|
The until operator provides another way to move forward, this time while
putting a requirement on the cycles in which we are moving. For example,
Assertion 2.8a states that whenever signal req is asserted, then, starting at
the next cycle, signal busy must be asserted up until signal done is asserted.
Assertion 2.8a requires that busy will be asserted up to, but not necessarily
including, the cycle where done is asserted. In order to include the cycle where
done is asserted, use the operator until_. The underscore (_) is intended to
represent the extra cycle in which we require that busy should stay asserted,
so Assertion 2.8b states that whenever signal req is asserted, then starting
from the next cycle, busy must be asserted and must stay asserted up until
and including the cycle where done is asserted. For example, Assertion 2.8a
holds on Trace 2.8(i), but Assertion 2.8b does not, because busy is not asserted at cycles 4 and 10. Both Assertions 2.8a and 2.8b hold on Trace 2.8(ii):
Assertion 2.8a does not prohibit the assertion of busy at cycles 4 and 10 – it
just does not require it.
If signal done is asserted the cycle after signal req is asserted, Assertion 2.8a does not require that signal busy be asserted at all, while Assertion 2.8b does. That is, Assertion 2.8a holds on Trace 2.8(iii) – the fact that
done happens immediately after req leaves no cycles on which busy needs to
be asserted. Assertion 2.8b does not hold on Trace 2.8(iii) because of a missing
assertion of busy in the cycle in which done is asserted.
|
|---|
assert always (req -> next (busy until done)); (2.8a) assert always (req -> next(busy until_ done)); (2.8b) |
Fig. 2.8: The until and until_ operators
|
The before family of operators provides an easy way to state that we
require some signal to be asserted before some other signal. For example, suppose that we have a pulsed signal called req, and we have the requirement that
before we can make a second request, the first must be acknowledged. We can
express this in PSL using Assertion 2.9a. We need the next to take us forward
one cycle so that the req in (ack before req) is sure to refer to some other
req, and not the one we have just seen. To understand this, let us examine a
flawed version of the same specification. Consider Assertion 2.9b. It requires
that (ack before req) hold at every cycle in which req holds. Consider,
for example, cycle 1 of Trace 2.9(i). Signal req is asserted. Therefore, (ack before req) must hold at cycle 1. However, it does not, because starting at
cycle 1 and looking forward, we first see an assertion of signal req (at cycle 1),
and only afterwards an assertion of signal ack (at cycle 3) – so req is asserted
before ack, and not the other way around. Assertion 2.9a, on the other hand,
states what we want: at cycle 1, for example, we require next (ack before req) to hold. Therefore, we require that (ack before req) hold at cycle 2.
Starting at cycle 2 and looking forward, we first see an assertion of ack (at
cycle 3), and only afterwards an assertion of req (at cycle 6).
|
|---|
assert always (req -> next (ack before req)); (2.9a) assert always (req -> (ack before req)); (2.9b) assert always (req -> next (ack before_ req)); (2.9c) assert always (req -> (ack || next (ack before req))); (2.9d) |
Fig. 2.9 The before and before_ operators
|
The before operator requires that its first operand happen strictly before
its second. In order to specify that something must happen before or at the
same cycle as something else, use before_. The underscore (_) is intended
to represent the cycle in which we allow an overlap between the left and
right sides. For example, in order to specify that behavior like that shown
in Trace 2.9(i) is allowed, and that in addition behavior like that shown in
Trace 2.9(ii) is allowed, use Assertion 2.9c.
What if the assertion of ack is allowed to come, not together with the next
assertion of req, but rather together with the request being acknowledged?
In other words, what if in addition to the behavior shown in Trace 2.9(i), we
want to allow the behavior shown in Trace 2.9(iii)? As we have seen previously,
Assertion 2.9b is not the answer. Rather, we can code Assertion 2.9d.
2.5 eventually!
The eventually! operator allows you to specify that something must occur in
the future without saying exactly when. For example, Assertion 2.10a states
that every request (assertion of req) must be followed at some time with
an acknowledge (assertion of ack). There is nothing in Assertion 2.10a to
prevent a single acknowledge from satisfying the requirement for multiple
requests, thus Assertion 2.10a holds on Trace 2.10(i). We examine the issue
of specifying a one-to-one correspondence between signals in Section 13.4.2.
The exclamation point (!) of the eventually! operator indicates that it
is a strong operator. We discuss weak vs. strong temporal operators in detail
in Chapter 4.
|
|---|
| (i) Assertion 2.10a holds |
assert always (req -> eventually! ack); (2.10a) |
Fig. 2.10: The eventually! operator
|
