PSL/A Practical Introduction to PSL/Some Philosophy/ru — различия между версиями
ANA (обсуждение | вклад) м (→3.3 Designs and traces) |
Valentin (обсуждение | вклад) (→Some Philosophy) |
||
| Строка 2: | Строка 2: | ||
| − | == | + | == Немного философии == |
| − | + | ||
| + | <!-- | ||
We have seen some basic PSL and gotten a feel for how it is intended to be | We have seen some basic PSL and gotten a feel for how it is intended to be | ||
used. Before we continue, we discuss some of the concepts at the root of PSL. | used. Before we continue, we discuss some of the concepts at the root of PSL. | ||
| + | --> | ||
| + | Мы рассмотрели немного основ PSL и получили ощущение того, как используется. Перед тем как продолжить, мы обсудим некоторые концепции в корне PSL. | ||
| + | === 3.1 Утверждения против свойств === | ||
| − | + | <!-- | |
| − | + | ||
As we have seen, a PSL assertion is made up of the keyword assert plus | As we have seen, a PSL assertion is made up of the keyword assert plus | ||
the PSL ''property'' being asserted, followed by a semi-colon. For example, in | the PSL ''property'' being asserted, followed by a semi-colon. For example, in | ||
| Строка 25: | Строка 27: | ||
sub-property of a more complicated property, and as such, it does not state a | sub-property of a more complicated property, and as such, it does not state a | ||
requirement on its own. | requirement on its own. | ||
| − | + | --> | |
| + | Как мы уже видели, утверждения PSL состоят из ключевого слова assert плюс ''свойства'' PSL для утверждения, разделенных точкой с запятой. Например, в утверждении <code>assert always (a -> next b);</code>, свойство - <code>always (a -> next b)</code>. Свойство выполняется или не выполняется в данном тракте. Утверждение, с другой стороны, указывает программе верификации, что свойство было утверждено, и требуется выполнение. Далее в книге мы будем внимательно рассматривать отличия между свойствами, которые просто описывают поведения, и утверждения,которые устанавливают требования. | ||
=== 3.2 The notion of time === | === 3.2 The notion of time === | ||
Версия 14:59, 13 ноября 2013
- 1. Introduction (en)
- 2. Basic Temporal Properties (en)
- 3. Some Philosophy (en)
- 4. Weak vs. Strong Temporal Operators (en)
- 5. SERE Style (en)
Содержание |
Немного философии
Мы рассмотрели немного основ PSL и получили ощущение того, как используется. Перед тем как продолжить, мы обсудим некоторые концепции в корне PSL.
3.1 Утверждения против свойств
Как мы уже видели, утверждения PSL состоят из ключевого слова assert плюс свойства PSL для утверждения, разделенных точкой с запятой. Например, в утверждении assert always (a -> next b);, свойство - always (a -> next b). Свойство выполняется или не выполняется в данном тракте. Утверждение, с другой стороны, указывает программе верификации, что свойство было утверждено, и требуется выполнение. Далее в книге мы будем внимательно рассматривать отличия между свойствами, которые просто описывают поведения, и утверждения,которые устанавливают требования.
3.2 The notion of time
When a Boolean assertion is embedded in code that is being run, like in the simple assertions of Java and (simulated) VHDL, the notion of time need not be defined – an assertion is checked whenever the statement containing the assertion is executed. For the more complicated assertions of PSL, which first of all stand apart from the code (so that the notion of “execution” is foreign to them) and which second of all span multiple time steps, the notion of time must be given more consideration.
PSL assumes that time is discrete, that is, that time consists of a sequence of evaluation cycles. The meaning of a PSL property is defined relative to such a sequence of cycles. In this book, we will refer to such a sequence of cycles as a trace.
PSL does not dictate how time ticks – that is, it does not dictate how such a sequence of cycles is extracted from a design under verification. This means that the sequence of cycles as seen by two verification tools is not necessarily the same. For example, a cycle-based simulator sees a sequence of signal values calculated cycle-by-cycle, while an event-based simulator running on the same design sees a more detailed sequence of signal values.
Nevertheless, there is a way to ensure that the meaning of a PSL property is not affected by the granularity of time as seen by the verification tool. PSL properties can be modified by using a clock expression to indicate that time should be measured in clock cycles of the clock expression. In the case of a clocked property, the result of a cycle-based tool will be the same as the result of an event-based tool. PSL allows the specification of a default clock, so that the clock does not have to be mentioned explicitly for each and every property. In most of this book we have assumed a singly clocked design under the cycle-based model, and thus most examples omit the explicit mention of the clock. Clocks are discussed in detail in Chapters 6 and 14.
3.3 Designs and traces
The purpose of a PSL property is to describe the desired behavior of a design. In order to do so, it is usually convenient to examine individual traces of that design. The Foundation Language (FL), which we focus on in this book, uses this approach, and thus throughout most of this book we shall be interested in whether or not a particular PSL property holds on a particular trace. The Foundation Language is suitable for both static (formal) and dynamic (simulation-based) verification.
Another approach, used by the Optional Branching Extension (OBE), uses a tree structure that represents multiple paths. This approach is applicable only to formal verification, and is touched on very briefly in Chapter 11.
3.4 Current cycle, sub-traces, and modularity
When a PSL property composed of two or more sub-properties is checked on a trace, it is sometimes necessary to decide the meaning of the sub-properties on a sub-trace. The current cycle is the name we give to the first cycle of a trace or a sub-trace on which we are evaluating a property or a sub-property.
Assuming that the cycles of a trace are numbered starting from 0, the current cycle of an assertion is 0. The current cycle of a sub-property of some enclosing property depends on its use in the enclosing property. The operands of a Boolean operator have the same current cycle as the parent property. The operands of a temporal operator have a current cycle that is related to the current cycle of the parent property in a way dictated by the temporal operator. For example, the next operator increases the current cycle by one, the always operator creates “multiple instances” of the sub-property, each of which has a current cycle that corresponds either to the current cycle or to some future cycle, etc.
NOTE: It is very important to understand that the term “multiple instances”
is intended to convey an intuition which is useful in understanding
the always operator. It is not intended to hint that any actual instantiation
is taking place; neither does it imply that a tool implementing PSL needs to
create multiple instances of an assertion checker, spawn multiple instances of
a process, or in any other way cause the words “multiple instances” to correspond
to actual instances of anything whatsoever. On the contrary, there are
many efficient implementations of PSL in which the always operator does not
create, spawn, or in any other way generate actual multiple instances. Still,
the term “multiple instances” is a good way to gain intuition about how the
always operator works, and a naive and inefficient implementation may well
generate multiple instances of a checker or of a process.
Getting back to our main point, consider the assertion assert always (a -> next b);. The current cycle of always (a -> next b) is 0. Whether or
not always (a -> next b) holds at cycle 0 depends on whether or not the
sub-property (a -> next b) holds at every cycle from 0 onwards. The current
cycle for a particular evaluation of the sub-property (a -> next b) will be
some cycle N. Finally, in order to determine whether or not sub-property
(a -> next b) holds at cycle N, we will need to evaluate sub-properties a
and next b with a current cycle of N, which means that we need to evaluate
sub-property b with a current cycle of N + 1.
To make the discussion more concrete, let’s consider our assertion, Assertion
3.1a, on Trace 3.1(i). Signal a holds in cycles 4 and 8. Signal b holds in
cycle 5, and therefore next b holds in cycle 4. This is shown in Trace 3.1(ii),
an annotated version of Trace 3.1(i). Since a holds in cycles 4 and 8, and next b
holds in cycle 4, we get that (a -> next b) holds in all cycles but cycle 8,
as shown in Trace 3.1(ii). (Remember that the else-part defaults to true, so (a -> next b)
holds in all cycles where a does not hold, and in addition in all
cycles where a holds and next b does too.) The entire property always (a -> next b)
therefore holds in cycles 9, 10, 11, 12 and 13 (because in these
cycles, (a -> next b) holds “now” and in all future cycles). Thus, Assertion
3.1a does not hold on Trace 3.1(i) (because it does not hold on cycle 0 –
the first cycle of the trace).

|
|---|
assert always (a -> next b); (3.1a) |
| Fig. 3.1: A concrete example |
The above explanation seems straightforward. However, the idea of modularity
hides some subtle points – for example, that the value of the property
a is dependent only on the current cycle. Thus, Assertion 3.2a holds on
Trace 3.2(i), because signal a holds in cycle 0. If you want to express the fact
that a should hold in every cycle, you must use the always operator, as in
Assertion 3.2b. Assertion 3.2b does not hold on Trace 3.2(i).
Another subtle point is that a property can hold on a suffix of a trace
without holding on the trace itself. Thus, the property always a holds on
the sub-traces of Trace 3.2(i) starting at cycles 12, 13, and 14. This would
be important if we used the property always a as a sub-property of some
other property. For example, Assertion 3.2c holds on Trace 3.2(i) because the
property always a holds on the 12th next cycle.
Finally, the cycles involved in calculating the left-hand side of a logical
implication may overlap those involved in calculating the right-hand side of
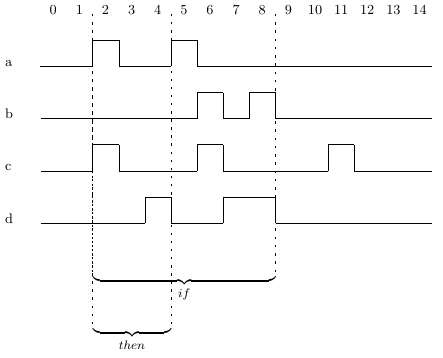
a logical implication. For example, consider Assertion 3.3a on Trace 3.3(i).
Assertion 3.3a holds on Trace 3.3(i) because the sub-property (a && next[6] (b)) -> (c && next[2] (d))
holds at all cycles. It holds at cycle 2 because
the left-hand side (a && next[6] (b)) holds and in addition the right-hand
side (c && next[2] (d)) holds. It holds at all other cycles because if the
“if” part of a logical implication does not hold, then the “else” part defaults
to true.

|
|---|
| (i) Assertions 3.2a and 3.2c hold, but 3.2b does not |
assert a; (3.2a) assert always a; (3.2b) assert next[12] (always a); (3.2c) |
| Fig. 3.2: The importance of the always operator |
Previously, for example in examining Assertions 2.2a and 2.3b, we have
seen cases where there is an overlap between the cycles involved in satisfying
two different occurrences of the left-hand side of a logical implication. These
overlaps are caused by the presence of the always operator in the property.
If we remove the always operator, the issue of overlap disappears from Assertions
2.2a and 2.3b. The overlap of Assertion 3.3a is different from the overlap
of Assertions 2.2a and 2.3b in a very important way: Assertion 3.3a is written
in such a way that the cycles involved in calculating the left-hand side of the
logical implication overlap those involved in calculating the right-hand side of
the logical implication: calculating the “if” part of the logical implication involves
examining the current cycle and also “looking ahead” six cycles, while
calculating the “then” part of the logical implication involves examining the
current cycle and also “looking ahead” two cycles. Thus the overlap results
from the logical implication itself. This style of PSL property is usually very
confusing to new users of PSL, and indeed it is not an intuitive way to use
the language. For this reason, such properties are not recommended, and the
simple subset of PSL restricts the language in such a way that such properties
are not allowed. We discuss the simple subset in more detail later. For now,
remember that if you have written a property in which the cycles involved in
calculating the left-hand side of an operator overlap for more than one cycle
with those involved in calculating the right-hand side of the same operator,
you have not written a property that is in the simple subset.
3.5 Reporting a failure
Consider Assertion 3.4a on the traces shown in Figure 3.4. Obviously, Assertion
3.4a does not hold on them. Now consider four different verification tools,
each of which reports the failure of Assertion 3.4a as indicated by the signal
called “failure” in Traces 3.4(i), 3.4(ii), 3.4(iii) and 3.4(iv). Tool 1 reports a
failure at cycle 4, the earliest that it can be detected. Tool 2 reports a failure
at cycle 4, but also at cycle 7, when b is asserted for a second time. Tool 3
reports a failure at the end of the trace, and Tool 4 reports a failure at cycle
1, when a is asserted.
Which tool is correct? The answer is that they all are. PSL defines whether or not a property holds on a trace – that is all. It says nothing about when a tool, dynamic or static, should report on the results of the analysis. Thus, there is no meaning in asking whether Tool 1, 2, 3 or 4 is correct. All of them indicate that the property fails on the trace, so all are correct. The failure indications shown along the trace can be thought of as debugging aids, hinting to the user where to look along the trace for the failure. As far as PSL is concerned, as long as a tool indicates correctly whether or not a property holds on a trace, it has done its job.

|
|---|
assert always (a -> never b); (3.4a) |
| Fig. 3.4: Four different tools reporting the failure of Assertion 3.4a on the same trace |