PSL/A Practical Introduction to PSL/Basic Temporal Properties — различия между версиями
ANA (обсуждение | вклад) (Новая страница: «{{PSL TOC}} ==Basic Temporal Properties While== While the Boolean layer consists of Boolean expressions that hold or do not hold at a given cycle, the temporal l…») |
ANA (обсуждение | вклад) м (→2.1 The always and never operators) |
||
| Строка 73: | Строка 73: | ||
Both Assertion 2.1b and Assertion 2.1c state that signals a and b are | Both Assertion 2.1b and Assertion 2.1c state that signals a and b are | ||
| − | mutually exclusive. Obviously, anything that can be stated with the always | + | mutually exclusive. Obviously, anything that can be stated with the <code>always</code> |
operator can be stated with the never operator and vice versa, simply by | operator can be stated with the never operator and vice versa, simply by | ||
| − | negating the operand when switching between always and never. PSL provides | + | negating the operand when switching between <code>always</code> and <code>never</code>. PSL provides |
both operators for convenience, as sometimes it is more natural to state | both operators for convenience, as sometimes it is more natural to state | ||
the property in the positive (that is, stating what must hold at all cycles) | the property in the positive (that is, stating what must hold at all cycles) | ||
| Строка 81: | Строка 81: | ||
general, there are many ways to state any property in PSL. We will see other | general, there are many ways to state any property in PSL. We will see other | ||
examples throughout the rest of this book. | examples throughout the rest of this book. | ||
| − | |||
===2.2 The next operator=== | ===2.2 The next operator=== | ||
Версия 14:25, 25 октября 2013
- 1. Introduction (en)
- 2. Basic Temporal Properties (en)
- 3. Some Philosophy (en)
- 4. Weak vs. Strong Temporal Operators (en)
- 5. SERE Style (en)
Содержание |
Basic Temporal Properties While
While the Boolean layer consists of Boolean expressions that hold or do not
hold at a given cycle, the temporal layer provides a way to describe relationships
between Boolean expressions over time. A PSL assertion typically looks
in only one direction – forwards from the first cycle (although it is possible
to look backwards using built-in functions such as prev(), rose() and
fell()). Thus, the simple PSL assertion assert a; states that a should hold
at the very first cycle, while the PSL assertion assert always a; states that
a should hold at the first cycle and at every cycle following the first cycle –
that is, at every cycle.
By combining the temporal operators in various ways we can state properties
such as “every request receives an acknowledge”, “every acknowledged
request receives a grant within four to seven cycles unless the request is canceled
first”, “two consecutive writes should not be to the same address”, and
“when we see a read request with tag equal to i, then on the next four data
transfers we expect to see a tag of i”.
The temporal layer is composed of the Foundation Language (FL) and the Optional Branching Extension (OBE). The FL is used to express properties of single traces, and can be used in either simulation or formal verification. The OBE is used to express properties referring to sets of traces, for example “there exists a trace such that ...”, and is used in formal verification. In this book we concentrate on the Foundation Language.
The Foundation Language itself is composed of two complementary styles – LTL style, named after the temporal logic LTL on which PSL is based, and SERE style, named after PSL’s Sequential Extended Regular Expressions, or SEREs. In this chapter we present the basic temporal operators of LTL style. We provide only a taste – enough to get the basic idea and to give some context to the philosophical issues that we discuss next.
Throughout this book, we make extensive use of examples. Each example property or assertion and its associated timing diagram (which we term a trace) are grouped together in a figure. Such a figure will contain one or more traces numbered with a parenthesized lower case Roman numeral, and one or more properties numbered by appending a lower case letter to the figure number. For instance, Figure 2.1 contains Trace 2.1(i) and Assertions 2.1a, 2.1b, and 2.1c.
2.1 The always and never operators
We have already seen the basic temporal operators always and never. Most
PSL properties will start with one or the other. This is because a “bare”
(Boolean) PSL property refers only to the first cycle of a trace. For example,
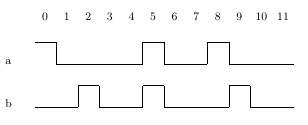
Assertion 2.1a requires only that the Boolean expression !(a && b) hold at
the first cycle. Thus, Assertion 2.1a holds on Trace 2.1(i) because the Boolean
expression !(a && b) holds at cycle 0. In order to state that we want it to
hold at every cycle of the design, we must add the temporal operator always
to get Assertion 2.1b. Assertion 2.1b does not hold on Trace 2.1(i) because
the Boolean expression !(a && b) does not hold at cycle 5. Equivalently, we
could have swapped the always operator and the Boolean negation ! with
never, to get Assertion 2.1c.
|
|---|
| (i) Assertion 2.1a holds, but 2.1b and 2.1c do not |
assert !(a && b); (2.1a) assert always !(a && b); (2.1b) assert never (a && b); (2.1c) |
| Fig. 2.1: The always and never operators |
Both Assertion 2.1b and Assertion 2.1c state that signals a and b are
mutually exclusive. Obviously, anything that can be stated with the always
operator can be stated with the never operator and vice versa, simply by
negating the operand when switching between always and never. PSL provides
both operators for convenience, as sometimes it is more natural to state
the property in the positive (that is, stating what must hold at all cycles)
and sometimes in the negative (that is, what must not hold for any cycle). In
general, there are many ways to state any property in PSL. We will see other
examples throughout the rest of this book.
2.2 The next operator
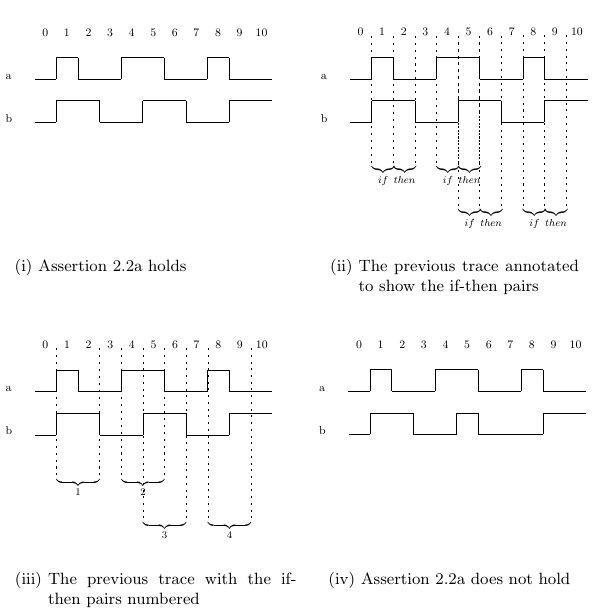
Another temporal operator is the next operator. It indicates that the property will hold if its operand holds at the next cycle. For instance, Assertion 2.2a states that whenever a holds, then b should hold in the next cycle. Assertion 2.2a uses another important operator, the logical implication operator (->). While the logical implication operator is a Boolean and not a temporal operator (it does not link two sub-properties over time), it plays a very important role in many temporal properties. A logical implication prop1 -> prop2 holds if either prop1 does not hold or prop2 holds. A good way to think of it is like an if-then expression, with the else-part being implicitly true. That is, prop1 -> prop2 can be understood as “if prop1 then prop2 else true”. Thus, the sub-property a -> next b in our example holds if either a does not hold (because then the property defaults to true) or if a holds and also next b holds. By adding an always operator, we get a property that holds if the sub-property a -> next b holds at every cycle. Thus, Assertion 2.2a states that whenever a holds, b must hold at the next cycle. Assertion 2.2a holds on Trace 2.2(i) because every assertion of signal a is followed by an assertion of signal b. This is shown in the “if” and “then” annotations on Trace 2.2(ii). The “additional” assertions of signal b at cycles 1 and 10 are allowed by Assertion 2.2a, because it says nothing about the value of b in cycles other than those following an assertion of a.
Note that the cycles involved in satisfying one assertion of signal a may overlap with those involved in satisfying another assertion. For example, consider Trace 2.2(iii), which is simply Trace 2.2(ii) with the if-then pairs numbered. There are four assertions of signal a on Trace 2.2(iii), and thus four associated cycles in which b must be asserted. Each pair of cycles (an assertion of a followed by an assertion of b) is numbered in Trace 2.2(iii). Consider pairs 2 and 3. Signal a is asserted at cycle 4 in pair 2, thus signal b needs to be asserted at cycle 5 in order for Assertion 2.2a to hold. Signal a is asserted at cycle 5 in pair 3, thus requiring that signal b be asserted at cycle 6. Pairs 2 and 3 overlap, because while we are looking for an assertion of signal b at cycle 5 in order to satisfy the assertion of a at cycle 4, we see an additional assertion of signal a that must be considered.
Assertion 2.2a does not hold on Trace 2.2(iv) because the third assertion of signal a, at cycle 5, is missing an assertion of signal b at the following cycle.
|
|---|
assert always (a -> next b); (2.2a) |
| Fig. 2.2: The next and logical implication operators |
2.3 Variations on next including next event
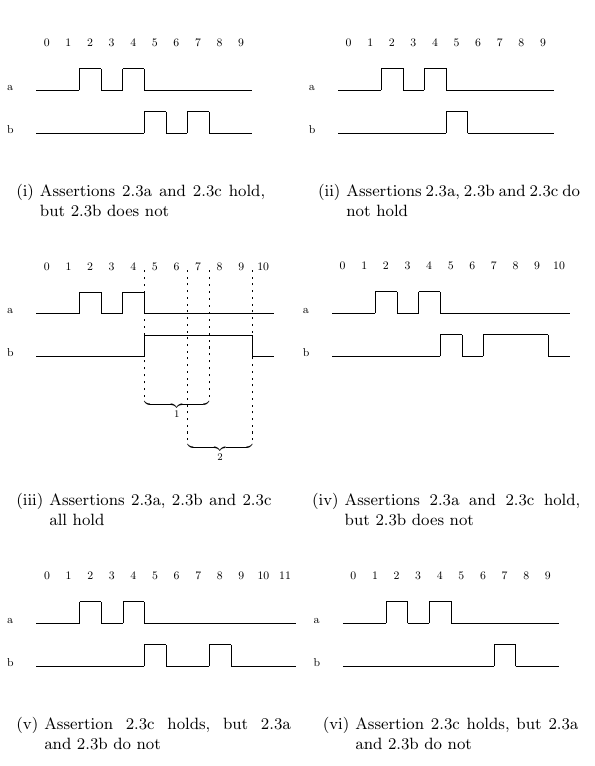
A next property holds if its operand holds in the next cycle. Variations on the next operator allow you to specify the nth next cycle, and ranges of future cycles. A next[n] property holds if its operand holds in the nth next cycle. For example, Assertion 2.3a states that whenever signal a holds, signal b holds three cycles later. Assertion 2.3a holds on Traces 2.3(i), 2.3(iii), and 2.3(iv), while it does not hold on Traces 2.3(ii) or 2.3(v) because of a missing assertion of signal b at cycle 7, and does not hold on Trace 2.3(vi) because of a missing assertion of signal b at cycle 5.
|
|---|
assert always (a -> next[3] (b)); (2.3a) assert always (a -> next a[3:5] (b)); (2.3b) assert always (a -> next e[3:5] (b)); (2.3c) |
Fig. 2.3: Операторы next[n], next_a[i:j] и next_e[i:j]
|
A next_a[i:j] property holds if its operand holds in all of the cycles from
the ith next cycle through the jth next cycle, inclusive. For example, Assertion
2.3b states that whenever signal a holds, signal b holds three, four and
five cycles later. It holds on Trace 2.3(iii) and does not hold on Traces 2.3(i),
2.3(ii), 2.3(iv), 2.3(v), or 2.3(vi).
Previously we discussed the fact that the cycles involved in satisfying one assertion of signal a may overlap those involved in satisfying another assertion of a. Trace 2.3(iii) has been annotated to emphasize this point for Assertion 2.3b. Signal b must be asserted in cycles 5 through 7 (marked as “1”) because of the assertion of a at cycle 2, and must be asserted in cycles 7 through 9 (marked as “2”) because of the assertion of a at cycle 4.
A next_e[i:j] property holds if there exists a cycle from the next i through the next j cycles in which its operand holds. For example, Assertion 2.3c states that whenever signal a holds, signal b holds either three, four, or five cycles later. There is nothing in Assertion 2.3c that prevents a single assertion of signal b from satisfying multiple assertions of signal a, thus it holds on Trace 2.3(vi) because the assertion of b at cycle 7 comes five cycles after the assertion of signal a at cycle 2, and three cycles after the assertion of signal a at cycle 4. We examine the issue of specifying a one-to-one correspondence between signals in Section 13.4.2.
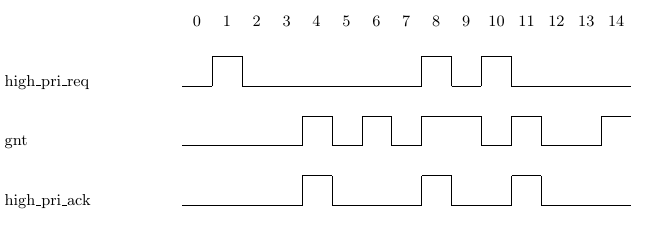
Assertion 2.3c also holds on Traces 2.3(i), 2.3(iii), 2.3(iv), and 2.3(v), since there are enough assertions of signal b at the appropriate times. In Traces 2.3(i), 2.3(iii), and 2.3(iv) there are more than enough assertions of b to satisfy the property being asserted (in Trace 2.3(i), the assertion of b at cycle 7 is enough, because it comes five cycles after the assertion of a at cycle 2, and three cycles after the assertion of a at cycle 4). In Trace 2.3(v) there are just enough assertions of b to satisfy the requirements of Assertion 2.3c. The next event operator is a conceptual extension of the next operator. While next refers to the next cycle, next event refers to the next cycle in which some Boolean condition holds. For example, Assertion 2.4a expresses the requirement that whenever a high priority request is received (signal high pri req is asserted), then the next grant (assertion of signal gnt) must be to a high priority requester (signal high pri ack is asserted). Assertion 2.4a holds on Trace 2.4(i). There are two assertions of signal high pri req, the first at cycle 1 and the second at cycle 10. The associated assertions of gnt occur at cycles 4 and 11, respectively, and high pri ack holds in these cycles.
The next_event operator includes the current cycle. That is, an assertion of b in the current cycle will be considered the next assertion of b in the property next event(b)(p). For instance, consider Trace 2.4(ii). Trace 2.4(ii) is similar to Trace 2.4(i) except that there is an additional assertion of high pri req at cycle 8 and two additional assertions of gnt at cycles 8 and 9, one of which has an associated high pri ack. Assertion 2.4a holds on Trace 2.4(ii) because the assertion of gnt at cycle 8 is considered the next assertion of gnt for the assertion of high pri req at cycle 8. If you want to exclude the current cycle, simply insert a next operator in order to move the current cycle of the next event operator over by one, as in Assertion 2.4b. Assertion 2.4b does not hold on Trace 2.4(ii). Because of the insertion of the next operator, the relevant assertions of gnt have changed from cycles 4, 8 and 11 for Assertion 2.4a to cycles 4, 9 and 11 for Assertion 2.4b, and at cycle 9 there is no assertion of high pri ack in Trace 2.4(ii).
Just as we can use next[i] to indicate the ith next cycle, we can use next event(b)[i] to indicate the ith occurrence of b. For example, in order to express the requirement that every time a request is issued (signal req is asserted), signal last ready must be asserted on the fourth assertion of signal ready, we can code Assertion 2.5a. Assertion 2.5a holds on Trace 2.5(i). For the first assertion of req, at cycle 1, the four assertions of ready happen to come immediately and in consecutive cycles. For the second assertion of req, at cycle 7, the four assertions of ready do not happen immediately and do not happen consecutively either – they are spread out over seven cycles, interspersed with cycles in which ready is deasserted. However, the point is that in both cases, signal last ready is asserted on the fourth assertion of ready, thus Assertion 2.5a holds on Trace 2.5(i).

|
|---|
| (i) Assertion 2.5a holds |
assert always (req -> (2.5a) next event(ready)[4](last ready)); |
| Fig. 2.5: next event[n] |
As with next a[i:j] and next e[i:j], the next event operator also
comes in forms that allow it to indicate all of a range of future cycles, or the existence
of a future cycle in such a range. The form next event a(b)[i:j](f)
indicates that we expect f to hold on all of the ith through jth occurrences
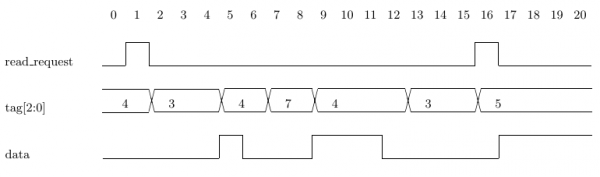
of b. For example, Assertion 2.6a indicates that when we see a read request
(assertion of signal read request) with tag equal to i, then on the next four
data transfers (assertion of signal data), we expect to see tag i. Assertion 2.6a
uses the forall construct, which we will examine in detail later. For now, suffice
it to say that Assertion 2.6a states a requirement that must hold for all
possible values of the signal tag[2:0]. Assertion 2.6a holds on Trace 2.6(i)
because after the first assertion of signal read request, where tag[2:0] has
the value 4, the value of tag[2:0] is also 4 on the next four assertions of
signal data (at cycles 5, 9, 10 and 11). Likewise, on the second assertion of
signal read request, where tag[2:0] has the value 5, the value of tag[2:0]
is also 5 on the next four assertions of signal data (at cycles 17 through 20).
In order to indicate that we expect something to happen on one of the next ith to jth cycles, we can use the next event e(b)[i:j](f) operator, which indicates that we expect f to hold on one of the ith through jth occurrences of b. For example, consider again Assertion 2.4a. It requires that whenever a high priority request is received, the next grant must be to a high priority requester. Suppose instead that we require that one of the next two grants be to a high priority requester. We can express this using Assertion 2.7a. Assertion 2.7a holds on Trace 2.7(i) because every time that signal high pri req is asserted, signal high pri ack is asserted on one of the next two assertions of gnt.
The syntax of the range specification for all operators – including those we have not yet seen – is flavor dependent. In the Verilog, SystemVerilog and SystemC flavors, it is [i:j]. In the VHDL flavor it is [i to j]. In the GDL flavor it is [i..j].
|
|---|
| (i) Assertion 2.6a holds |
assert forall i in {0:7}: (2.6a)
always ((read_request && tag[2:0]==i) ->
next_event_a(data)[1:4](tag[2:0]==i));
|
Fig. 2.6 next_event a[i:j]
|
2.4 The until and before operators

|
|---|
| (i) Assertion 2.7a holds |
assert always (high_pri_req -> (2.7a) next_event_e(gnt)[1:2](high_pri_ack)); |
Fig. 2.7: next_event e[i:j]
|

|
|---|
assert always (req -> next (busy until done)); (2.8a) assert always (req -> next(busy until_ done)); (2.8b) |
Fig. 2.8: The until and until_ operators
|

|
|---|
| (i) Assertion 2.10a holds |
assert always (req -> eventually! ack); (2.10a) |
Fig. 2.10: The eventually! operator
|