Литература

Введение в PSL

Содержание

1 SERE Style

SERE Style

Up until now, we have seen PSL properties that are built of Boolean expres- sions and temporal operators in LTL style. Another way to build properties is to use SEREs – Sequential Extended Regular Expressions. SEREs are similar in spirit to standard regular expressions, like those used for pattern matching in many applications. One difference is that the atoms of a SERE are Boolean expressions, whereas the atoms of a standard regular expression are single characters.

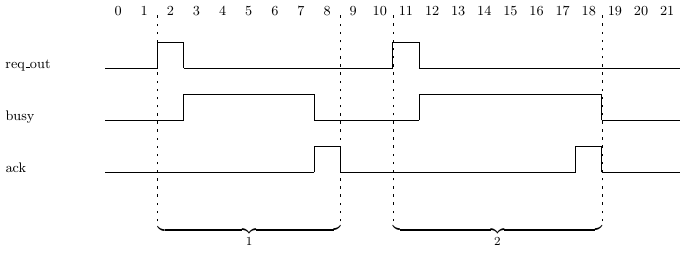
A SERE is typically enclosed in curly braces, and the atoms of the SERE are typically separated by semi-colons. For instance, {a;b;c} is a SERE, and SERE 5.1a is a more complicated SERE. SERE 5.1a describes a sequence of cycles in which (req out && !ack) is asserted on the first cycle, then (busy && !ack) is asserted for zero or more cycles, indicated by the consecutive repetition operator [*], and finally ack is asserted. Thus, SERE 5.1a matches the sequence of cycles labeled as “1” in Trace 5.1(i). Don’t be tempted into reading more into a SERE than is actually there: SERE 5.1a matches the sequence of cycles labeled as “2” in Trace 5.1(i) as well. SERE 5.1a does not prohibit the assertion of busy during the last cycle of the SERE. If it is important to exclude such behavior, busy must be mentioned explicitly, as shown in SERE 5.1b. SERE 5.1b matches the sequence of cycles labeled as “1” shown in Trace 5.1(i), but does not match the sequence of cycles labeled as “2” in that trace.

How is a SERE used? First, since a SERE is a property, it can be used as a sub-property. For example, Property 5.2a holds if whenever there is an assertion of req in && gnt then starting on the next cycle we see a sequence of cycles matching SERE 5.1a. Property 5.2a holds on Trace 5.2(i).

NOTE: A SERE is a property, but a property is not a SERE. Thus, while you can use a SERE as an operand of a temporal operator, you cannot embed a temporal operator such as always or next inside of a SERE.

Suppose now that we have a situation similar to that of Property 5.2a, but in which a grant (assertion of signal gnt) is given the cycle after the assertion of req in. We could try to replace the Boolean expression req in && gnt with the temporal expression req in && next gnt, as in Property 5.3a. However, remember the lesson of Section 3.4: in Property 5.3a the current cycle of the left-hand side (req in && next gnt) is the same as the current cycle of the right-hand side (because they are connected by the Boolean operator ->). Thus, the current cycle of gnt (which is the operand of a next operator) is the same as the current cycle of the SERE (which is also the operand ofnext operator). This is slightly confusing, and indeed Property 5.3a is not in the simple subset of PSL discussed in Chapter 9.

Let’s modify Property 5.3a as shown in Property 5.3b. Now a single next operator is applied to both gnt and the SERE, which are both operands of the -> operator. Property 5.3b is equivalent to Property 5.3a, but is in the simple subset, making the timing between gnt and the SERE easier to see. If we mean that the current cycle of the SERE should be the cycle after that of gnt, we can manipulate Property 5.3b by adding a next as in Property 5.3c. However, the suffix implication operators provide a much easier way.


(i) SERE 5.1a matches both 1 and 2. SERE 5.1b matches 1, but not 2.
{(req_out && !ack) ; (busy && !ack)[] ; ack} (5.1a) {(req_out && !ack) ; (busy && !ack)[] ; ack && !busy} (5.1b)
Fig. 5.1: Two simple SEREs


(i) Property 5.2a holds
always ((req_in && gnt) -> (5.2a) next {(req_out && !ack) ; (busy && !ack)[*] ; ack})
Fig. 5.2: A SERE is a property

always ((req_in && next gnt) ->                            (5.3a)
   next {(req_out && !ack) ; (busy && !ack)[*] ; ack})
always (req_in -> next (gnt ->                             (5.3b)
   {(req_out && !ack) ; (busy && !ack)[*] ; ack}))
always (req_in -> next (gnt ->                             (5.3c)
   next {(req_out && !ack) ; (busy && !ack)[*] ; ack}))

Fig. 5.3: Property 5.3a is not in the simple subset. Properties 5.3b and 5.3c are in the simple subset, but are difficult to read. These properties can be expressed more easily using suffix implication.

5.1 Suffix implication (|-> and |=>)

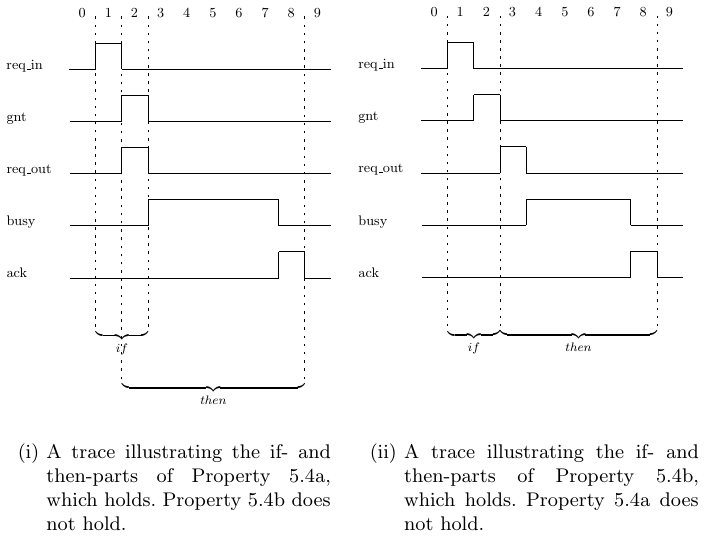
The suffix implication operators (|-> and |=>) provide a way to link two SEREs in such a way that the right-hand side starts when the left-hand side finishes. The overlapping suffix implication operator (|->) interprets “when the left-hand side finishes” as “at the same cycle as the cycle in which the left-hand side finishes”, while the non-overlapping suffix implication operator (|=>) interprets it as “the cycle after the cycle in which the left-hand side fin- ishes”. Thus, Property 5.4a is equivalent to Property 5.3b, and Property 5.4b is equivalent to Property 5.3c. Both Property 5.4a and Property 5.4b are eas- ier to grasp than the equivalent property without suffix implication, and both belong to the simple subset, discussed in Chapter 9.

Recall that the logical implication operator (->) can be understood as an if-then expression, with the else-part being implicitly true. The suffix implica- tion operators (|-> and |=>) can be understood the same way. The difference between the logical implication operator (->) and the suffix implication op- erators (|-> and |=>) is in the timing relationship between the if- and the then-parts. While the current cycle of the then-part of a logical implication operator (->) is the same as the current cycle of its if-part, the current cycle of the then-part of a suffix implication operator (|-> or |=>) is the first cycle of the suffix of the trace that remains once the if-part has been seen. This is illustrated for Properties 5.4a and 5.4b in Traces 5.4(i) and 5.4(ii).

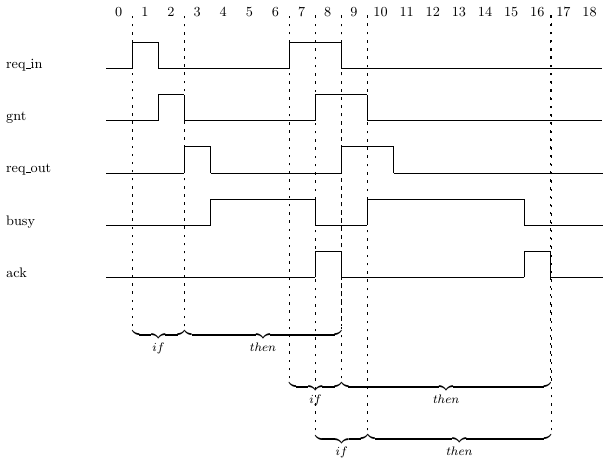
In Traces 5.4(i) and 5.4(ii) there is a single assertion of signal req in. If there are multiple assertions of req in, then of course we will be able to identify multiple if-then pairs, as shown in Trace 5.5(i). Note that the if-part of another if-then pair may begin before the if-part or the then-part of a previous if-then pair has completed. For instance, the second if-then pair starts at cycle 7, before the then-part of the first if-then pair has completed. The third if- then pair starts at cycle 8, before the then-part of the first if-then pair has completed, and before the if-part of the second if-then pair has completed. We have seen this kind of overlapping previously, in Traces 2.2(ii) and 2.3(iii). Note that in Trace 5.5(i), the assertion of ack at cycle 16 completes the then- part of the second and of the third if-then pair. For a deeper discussion of this phenomenon, see Section 13.4.2.

Properties 5.6a and 5.6b hold on Trace 5.6(i) because there is no sequence of cycles matching the left-hand side, thus the else-parts default to true at every cycle.

5.2 Weak and strong SEREs

Like temporal operators, SEREs come in weak and strong versions, and like temporal operators, the strong version of a SERE is indicated by an exclama- tion point (!). Thus, Property 5.7a, whose right-hand side is a weak SERE, holds even if signal ack is never asserted (as long as the rest of the SERE is not violated). Property 5.7b, whose right-hand side is a strong SERE, holds only if we eventually reach a cycle where ack occurs. In other words, the weak version of a SERE allows us to accept a trace that is “too short”, whereas the strong version requires that we “reach the end” of the SERE. Thus, while Property 5.7a holds on Trace 5.7(i) as well as Trace 5.7(ii), Property 5.7b, the strong version, holds on Trace 5.7(ii) but not on Trace 5.7(i).

5.2 Weak and strong SEREs

Like temporal operators, SEREs come in weak and strong versions, and like temporal operators, the strong version of a SERE is indicated by an exclama- tion point (!). Thus, Property 5.7a, whose right-hand side is a weak SERE, holds even if signal ack is never asserted (as long as the rest of the SERE is not violated). Property 5.7b, whose right-hand side is a strong SERE, holds only if we eventually reach a cycle where ack occurs. In other words, the weak version of a SERE allows us to accept a trace that is “too short”, whereas the strong version requires that we “reach the end” of the SERE. Thus, while Property 5.7a holds on Trace 5.7(i) as well as Trace 5.7(ii), Property 5.7b, the strong version, holds on Trace 5.7(ii) but not on Trace 5.7(i).

5.3 The never operator applied to a SERE

Another way to use a SERE is in describing sequences of events that should never happen. For example, Assertion 5.8a states that signal req should never be asserted for two consecutive cycles, and thus does not hold on Trace 5.8(i).

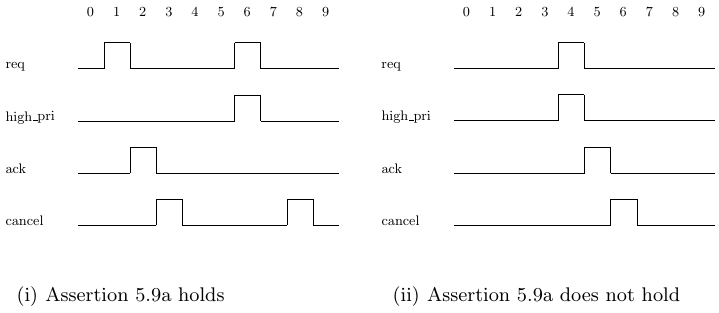
As another example, consider Assertion 5.9a. It states that an acknowl- edged high priority request (assertion of req together with high pri, followed a cycle later by ack) cannot be canceled (assertion of cancel the cycle after ack). Thus it holds on Trace 5.9(i), but not on Trace 5.9(ii).

5.4 SERE repetition operators ([*n], [=n], and [->n])

Up until now, we have seen basic SEREs composed of (possibly repeated) Boolean expressions separated by semi-colons. In this section, we examine SERE operators that allow you to build more sophisticated SEREs, using variations on the SERE repetition operators [*n], [=n], and [->n].

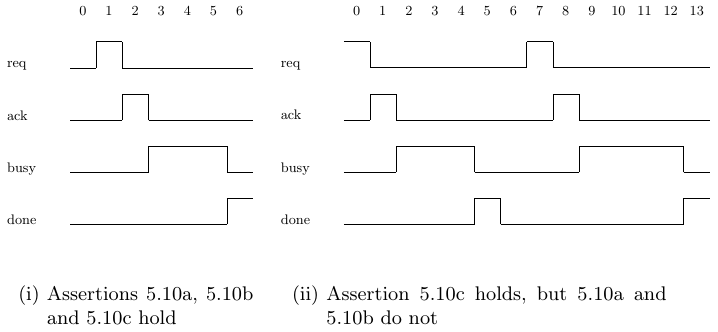
Consecutive repetition operators provide a shortcut to typing the same sub-SERE a number of times. The [*n] operator is an abbreviation for n repetitions of the SERE it is applied to. For example, instead of typing busy;busy;busy in Assertion 5.10a, we can use the abbreviation busy[*3], as in Assertion 5.10b. Assertions 5.10a and 5.10b state that after a request (assertion of signal req), we expect to see an acknowledge (assertion of signal ack) followed by three cycles in which signal busy is asserted, followed by an assertion of signal done. Trace 5.10(i) is an example of a trace on which Assertions 5.10a and 5.10b hold.

Instead of a specific number of repetitions, we can specify a range, i through j, like this: [*i:j]. Thus, Assertion 5.10c is similar to Asser- tion 5.10b, but instead of requiring exactly three assertions of signal busy, we require between three and five. Assertion 5.10c holds on Trace 5.10(i) as well as on Trace 5.10(ii).

The upper bound of a range can be infinity, which is indicated by a $ in the SystemVerilog flavor, by null in the GDL flavor, and by inf in the Verilog, VHDL, and SystemC flavors. For instance, the SERE {b[*5:inf]} matches five or more repetitions of b.

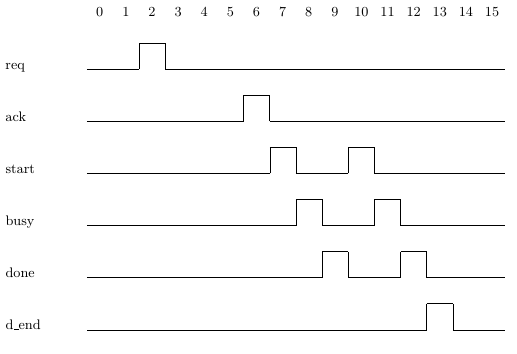
We can repeat not only a Boolean expression, but a SERE as well. For example, Property 5.11a holds if after an acknowledged request (an assertion of signal req followed by an assertion of signal ack), we see three data transfers followed by an assertion of signal d end, where a data transfer is an assertion of signal start followed by an assertion of signal busy followed by an assertion of signal done. Trace 5.11(i) is an example of a trace on which Property 5.11a holds.

If we omit the n, the resulting SERE matches any number of repetitions of the Boolean expression or SERE that is being repeated. For example, asserting Property 5.11b indicates that after an acknowledged request, we expect to see any number of data transfers followed by an assertion of done. Property 5.11b holds on Trace 5.11(i), as well as on Traces 5.11(ii) and 5.11(iii).

A [*] repetition matches any number of repetitions, including none. Thus, Property 5.11b holds on Trace 5.11(iv) as well. If you want to specify any non-zero number of repetitions, use the [+]. Thus, Property 5.11c is similar to Property 5.11b, but it requires at least one data transfer before signal done is asserted. Thus, Property 5.11c does not hold on Trace 5.11(iv), but it does hold on Traces 5.11(i), 5.11(ii) and 5.11(iii).

Instead of omitting the n, we can omit the Boolean expression or SERE and let the repetition [*n] stand alone. A stand-alone [*n] is equivalent to ‘true[*n]. In other words, [*n] matches any n cycles (because ‘true holds in all cycles). Another way to think of it is that it allows us to “skip” n cycles. Thus, Property 5.12a is similar to Property 5.11b, but instead of the acknowledge (assertion of signal ack) coming immediately following the request (assertion of signal req), it comes four cycles later. Property 5.12a holds on Trace 5.12(i).

The nonconsecutive repetition operator ([=n]) provides a way to describe repetitions that happen on not necessarily consecutive cycles. It can be ap- plied only to a Boolean expression. For example, to describe the requirement that after a request (assertion of signal req), we expect to see an acknowledge (assertion of signal ack) followed by some number of cycles including three not necessarily consecutive assertions of signal busy, followed by an asser- tion of signal done, we can code Assertion 5.13a. Assertion 5.13a holds on Trace 5.13(i). Note the cycles marked “busy[=3]” in Trace 5.13(i). They do not start with an assertion of busy, nor do they end with one. The noncon- secutive repetition operator [=n] will match any sequence of cycles in which there are n not necessarily consecutive repetitions of the Boolean expression being repeated, including sequences of cycles in which the “padding” is at the beginning and/or at the end. In other words, it will match any sequence of cycles in which the number of assertions of the Boolean expression being repeated is equal to n (thus the use of the equals sign in [=n]).

If you want to disallow the padding at the end, use the goto repetition op- erator [->n]. The goto repetition operator [->n] is similar to the nonconsec- utive repetition operator, except that the sequence of cycles being described ends with an assertion of the Boolean expression being repeated. In other words, it will match any sequence of cycles starting at the current cycle and ending after you “go to” the nth occurrence of the Boolean expression (the use of the -> is intended to remind you of an arrow instructing you to go to n). Thus Assertion 5.13b does not hold on Trace 5.13(i), but it does hold on Trace 5.13(ii) because the third busy is immediately followed by an assertion of signal done.

The n can be omitted for the goto repetition operator, in which case n defaults to 1. In other words, b[->] is equivalent to b[->1].

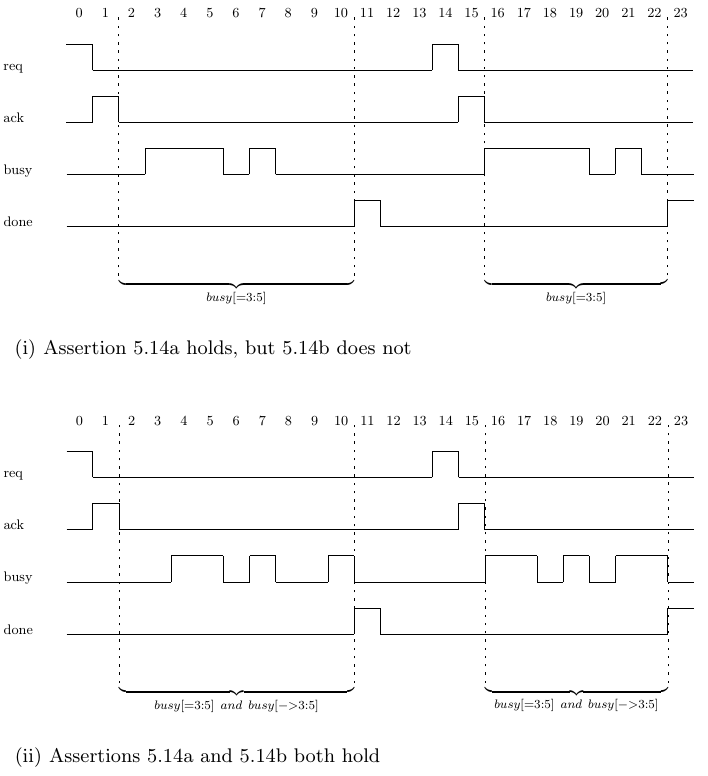
Like the consecutive repetition operators, the nonconsecutive repetition operator and the goto repetition operator can take a range. Thus, Asser- tion 5.14a requires three to five not necessarily consecutive assertions of busy after the assertion of signal ack and before the assertion of done, while Asser- tion 5.14b requires the same, and in addition that the assertion of signal done occur immediately after the 3rd, 4th, or 5th assertion of signal busy. Thus As- sertion 5.14a holds on Traces 5.14(i) and 5.14(ii), while Assertion 5.14b holds on Trace 5.14(ii) but not on Trace 5.14(i).

5.5 Concatenation (;) and fusion (:)

We have already seen the concatenation operator, a semi-colon, which is used to join two SEREs (or two Boolean expressions, or a Boolean expression and a SERE) in such a way that the right-hand SERE starts the cycle after the left-hand SERE ends. The fusion operator, a colon, is used to join two SEREs (or two Boolean expressions, or a Boolean expression and a SERE) in such a way that there is a single cycle of overlap between them: the right-hand SERE starts the same cycle that the left-hand SERE ends.

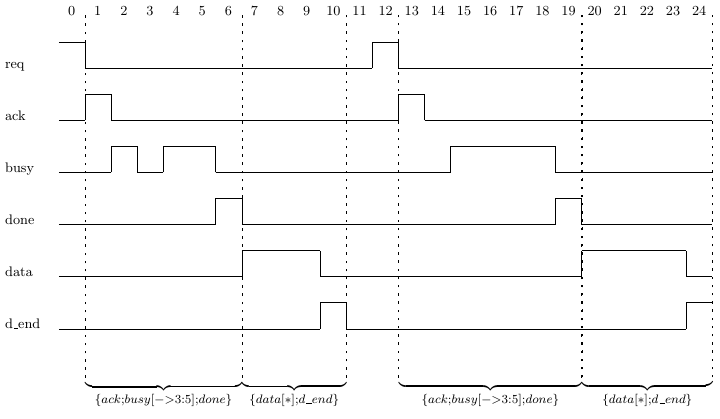
For example, consider the case that we want to specify the behavior of As- sertion 5.14b, and in addition, following the assertion of signal done, we should see a data transfer, which consists of the assertion of signal data for some num- ber of cycles (might be zero), followed by an assertion of signal d end. Using the concatenation operator, we can write Assertion 5.15a. Trace 5.15(i) is a trace on which Assertion 5.15a holds. The first assertion of signal req gets three cycles of data before the assertion of d end, while the second assertion of signal req sees four cycles of data before seeing d end.

If the data transfer should start the same cycle as signal done is asserted, then we can use the fusion operator as in Assertion 5.16a. Trace 5.16(i) is an example of a trace on which Assertion 5.16a holds. It is similar to Trace 5.15(i), except that the data transfer starts the same cycle as that in which done is asserted, rather than the cycle following the assertion of signal done.

Note that while it may be tempting to understand the concatenation op- erator (;) as a delay, the operator does not necessarily “eat” a cycle. For in- stance, in the case of the SERE {a ; b[*] ; c}, the b[*] may match zero, one, or more cycles, as illustrated in Trace 5.17(i). The first match shown in Trace 5.17(i) is only two cycles long, thus, the second concatenation operator (;) did not “eat” a delay. A better way to think of it is that concatenation gives you an ordered list of things to happen – some of them may consume one cycle, some more, and some no cycles at all.

Further note that fusion requires an overlap of at least one cycle. Thus, while the {b[*]} in {b[*] ; c} may match an empty sequence of cycles, replacing the concatenation operator with the fusion operator like this: {b[*]: c} results in a SERE with at least one assertion of b (otherwise there is nothing to overlap with the assertion of c). In both cases, the match may consist of a single cycle. The difference is that in the case of {b[*] ; c} the single cycle may not include an assertion of b (because there may be zero assertions of b preceding c), while in the case of {b[*] : c}, the single cycle must include an assertion of b (which overlaps with the assertion of c).

5.6 Compound SEREs

Compound SEREs are SEREs built from other SEREs through operations other than concatenation and fusion. The available operators allow you to “and” or “or” together two or more SEREs, as well as to express the situation where a match of one SERE occurs within a sequence of cycles matched by another.

Consider the case that we want to say that signal read complete is as- serted on the last data cycle of every read operation, where we have two kinds of read operations: a short read consists of an assertion of signal short rd fol- lowed by eight not necessarily consecutive assertions of data, and a long read consists of an assertion of signal long rd followed by 32 such assertions. We could code two separate properties, as shown in Properties 5.18a and 5.18b. Alternatively, we could use the SERE “or” operator (|) to “or” the two SEREs together, as in Property 5.18c.

The SERE “and” operator comes in two types: length-matching and non- length-matching. Both the length-matching (&&) and the non-length-matching (&) “and” operators match a sequence of cycles if starting at the current cycle, the left-hand side and the right-hand side are matched. The difference is that in addition, the length-matching “and” operator requires that the lengths of the sequences matched by both the left- and right-hand sides are the same, while the non-length-matching operator matches even if they are different. A length-matching “and” between SEREs R and S is illustrated in Trace 5.19(i), and a non-length-matching “and” between SEREs R and S is illustrated in Traces 5.20(i), 5.20(ii) and 5.20(iii).

When a non-length-matching “and” is used on the left-hand side of a con- catenation or a fusion, the current cycle of the right-hand side of the concate- nation or fusion is determined by the longer of the two subsequences making up the non-length-matching “and”. For instance, in the SERE {{{a;b[*5];c} & {d[*];e}} ; f}, the current cycle of f is the cycle after the cycle in which the longer of the two SEREs {a;b[*5];c} and {d[*];e} completes. This is illustrated in Traces 5.21(i) and 5.21(ii). Note that in each of the traces, sig- nal f is asserted twice: once after the completion of {a;b[*5];c}, and once after the completion of {d[*];e}. However, in each trace, only the assertion of signal f that happens after the completion of the longer of the two SEREs participates in the “match” of SERE {{{a;b[*5];c} & {d[*];e}} ; f}.

NOTE: A length-matching “and” such as {a;b;c} && {d} is legal, but makes no sense (because there is no sequence which is both 3 cycles long to match {a;b;c} and 1 cycle long to match {d}). Many tools will probably issue a warning for such a SERE.

As an example of the use of the length-matching “and”, consider the case that a read request (assertion of signal read req) that is granted (assertion of signal gnt within 5 cycles of the request) should be followed by a data transfer (assertion of signal data start followed by some number of consecutive as- sertions of data, followed by an assertion of data end), unless it is canceled. A cancel is an assertion of signal cancel any time between the assertion of read req and the assertion of gnt, inclusive. We can express this using As- sertion 5.22a. Assertion 5.22a holds on Trace 5.22(i): the first read request is followed by a data transfer, while the second read request is not followed by a data transfer, but is not required to be since it is canceled.

In the case of Assertion 5.22a, we needed the length-matching “and”. To see why, consider what would have happened had we used the non- length-matching “and” as in Assertion 5.22b. In the case of Assertion 5.22b, the left-hand side SERE {{read req ; [*0:4] ; gnt} & {cancel[=0]}} is matched not only by the sequence of cycles starting at cycle 2 and ending at cycle 5, but also by the sequences of cycles starting at cycle 2 and ending at any of the cycles 6 through 16. Thus, Assertion 5.22b requires that we see a data transfer starting not only at cycle 6, but also at cycles 7, 8, 9, 10 and so on. Obviously, this is not what we wanted.

As an example where we want the non-length-matching “and” rather than the length-matching “and”, consider the case that signal global print req indicates that we should see a print on each of printers 1, 2, and 3 (comple- tion of which is indicated by assertions of p1 done, p2 done, and p3 done, respectively), and that following completion of the last print job, we should see an assertion of signal print success. We can express this as shown in Assertion 5.23a. Assertion 5.23a holds on Trace 5.23(i) because following the assertion of signal global print req, we see assertions of each of the signals p1 done, p2 done and p3 done, the last of which is followed by an assertion of print success.

The non-length-matching “and” was needed for Assertion 5.23a. To see why, consider what would have happened if we had used the length-matching “and”, as in Assertion 5.23b. Assertion 5.23b does not hold on Trace 5.23(i) because the use of the length-matching “and” means that p1 done[->], p2 done[->] and p3 done[->] must all have the same length, i.e., that p1 done, p2 done and p3 done must all be asserted at the same time.

The SERE within operator is useful if you want to describe a situation where one SERE occurs within the time frame of another. For instance, sup- pose that the normal behavior of the design is to complete a high priority request first, even if there is a pending low priority request that started be- fore it. However, if signal no nesting is asserted when the low priority re- quest is issued, then this is prohibited. In other words, the situation shown in Trace 5.24(i) is not allowed. We can describe the prohibited situation as shown in Assertion 5.24a. Assertion 5.24a does not hold on Trace 5.24(i) because there is a match of {high pri begin ; high pri end[->]} that is entirely enclosed within the match of {(low pri begin && no nesting) ; low pri end[->]}.

NOTE: If the left and right operands of a within operator are s and t respectively, then the within operator is simply a shorthand for a length- matching “and” between {[*] ; s ; [*]} and {t}. That is, s within t is equivalent to {[*] ; s ; [*]} && {t}.

5.7 More about suffix implication

Up until now, we have seen the suffix implication operators (|-> and |=>) used with SEREs on both the left- and the right-hand sides. While the left- hand side of a suffix implication operator must be a SERE, the right-hand side of a suffix implication operator can be any property. Thus, if we want to express the requirement that whenever we have a request that is acknowledged (assertion of req followed by an assertion of ack) we should see a grant (assertion of signal gnt within three cycles of the acknowledge), we can code as in Assertion 5.25a.

This is illustrated in Trace 5.25(i). In the trace, there are three occurrences of the SERE {req;ack}. The first is followed by an assertion of ack after two cycles, the second after three cycles, and the third after a single cycle. Thus, Assertion 5.25a holds on the trace.

Of course, we could have written Assertion 5.25a entirely in SERE style, as shown in Assertion 5.25b, or entirely without SEREs, as in Assertion 5.25c. Assertions 5.25a, 5.25b and 5.25c are equivalent, thus the issue is purely one of style. Some people prefer using only one style, others find a mix of styles, depending on the particular property, to be easier to understand.

5.8 The built-in function ended()

The built-in function ended() takes a SERE as an argument and returns true in any cycle where that SERE has just ended.1 For example, Trace 5.26(i) has been annotated with a waveform labeled ended({a ; b[*] ; c}) to show the value of the call to ended() at each cycle.

1 - In previous versions of PSL, the role of the built-in function ended() was played by endpoints. Endpoints are no longer a part of the language – use built-in function ended() instead.

How is ended() used? Consider that a complete data transfer consists of an assertion of signal data start followed by some number of assertions of data, followed by an assertion of data end. Consider further that we have a signal data transfer complete that should be asserted when a data trans- fer is completed, and that we would like to specify the correct behavior of this signal. A good start would be Assertion 5.27a. Assertion 5.27a ensures that data transfer complete is asserted at the conclusion of every data transfer. But what about the other direction? That is, what about ensuring that whenever data transfer complete is asserted, a complete data trans- fer has indeed concluded? Assertion 5.27a does not ensure this, and thus it holds on Trace 5.27(i), even though there are “extraneous” assertions of data transfer complete at cycles 6 and 15. We would like an assertion that holds on Trace 5.27(ii) but not on 5.27(i).

In order to check the second direction (that there are no extraneous asser- tions of data transfer complete) we need to switch the direction of the implication: we need to say that if data transfer complete is asserted, then we have just seen the conclusion of a complete data transfer. We could try Assertion 5.27b. However, that doesn’t work. Assertion 5.27b requires that the SERE {data start ; data[*] ; data end} start the same cycle as data transfer complete, while we want it to end that cycle.

This is where the built-in function ended() comes in. Using ended(), we can code what we want as shown in Assertion 5.27c, which states that whenever we see an assertion of data transfer complete, we must have just seen the end of SERE {data start ; data[*] ; data end}, and it does not hold on Trace 5.27(i).

Note that ended() returns a Boolean value. Since the left-hand side of the suffix implication in Assertion 5.27c consists of a single Boolean expression, we could have coded Assertion 5.27c equivalently using logical implication as shown in Assertion 5.27d.

5.9 Overlapping matches of a SERE

Up until now, we have been concentrating on explaining the meaning of each SERE operator, using relatively simple examples. It is now time to introduce some more complex examples, in order to emphasize that like LTL style prop- erties, interpreting a SERE style property on a trace can involve examining overlapping sets of cycles.

Consider Property 5.28a on Traces 5.28(i) and 5.28(ii). There are multiple matches of {a ; b[*] ; c} on Trace 5.28(i), one match ending at cycle 2, one ending at cycle 3, and one ending at cycle 4. Property 5.28a does not hold on Trace 5.28(i), because the matches ending at cycles 2 and 3 do not have associated assertions of signal d at cycles 3 and 4. A suffix implication requires that for every match of the left-hand side, the right-hand side holds. Property 5.28a does hold on Trace 5.28(ii), because signal d is asserted after each match of {a ; b[*] ; c}.

Note that although Property 5.28a contains an always operator, the always operator is not the source of the overlapping matches in this case. Rather, for a single current cycle (cycle 1), there are three separate matches of the SERE {a ; b[*] ; c}, each ending at a different cycle.

The overlapping can happen on the right-hand side of a suffix implication as well. Consider for example Property 5.29a on Trace 5.29(i). There are three matches of {d ; e[*] ; f}, ending at cycles 3, 4, and 5. One match would have been enough to satisfy Property 5.29a, because as long as there exists one match, {d ; e[*] ; f} holds. The fact that there are in fact three matches does not hurt. Thus, Property 5.29a holds on Trace 5.29(i).

We have just explained that we require at least one match of the right-hand side for every match of the left-hand side of a suffix implication, and it might seem that in so doing, we have introduced something new. Actually, the rule could have been deduced from the parallel we have previously drawn between a suffix implication and an if-then statement. SERE {a ; b[*] ; c} can be understood as an infinite “or” between SEREs {a;c}, {a;b;c}, {a;b;b;c}, and so on. So Property 5.28a can be understood as “if {a;c} or {a;b;c} or {a;b;b;c} or ..., then d”, which clearly should hold only if we see a d every time the if-part is matched. And Property 5.29a can be understood as “if c, then {d;f} or {d;e;f} or {d;e;e;f} or ...”, which of course should hold as long as we have seen at least a single match of the then-part.